238. Product of Arrray Except Self

Vui lòng đọc hiểu đề trước khi đọc bài viết này tại đây:

https://leetcode.com/problems/product-of-array-except-self/description/

Table of Contents

1. Cách tiếp cận vấn đề

Yêu cầu của bài toán hết sức đơn giản, nhận vào 1 array input với chiều dài là n và trả về một array output với cùng chiều dài, trong đó giá trị ở vị trí i chính là tích của tất cả các số trong mảng input từ vị trí 0 đến n - 1 ngoại trừ số ở vị trí i.

Ví dụ với input: nums = [1,2,3,4] thì output sẽ là [2x3x4,1x3x4,1x2x4,1x2x3] = [24,12,8,6]

Một yêu cầu quan trọng nữa là ta cần phải giải bài này với độ phức tạp là O(n) và không được sử dụng phép chia. (n là số lượng phần tử trong mảng nums)

Cách làm đầu tiên mà ta có thể nghĩ ra đó chính là sử dụng kỹ thuật vét cạn BruteForce. Sử dụng 2 vòng lặp, 1 vòng lặp để cố định từng vị trí i trong mảng ouput, vòng lặp còn lại lần lượt đi qua các phần tử không phải tại vị trí i đang xét và nhân chúng lại với nhau. Tuy nhiên độ phức tạp của nó lại là O(n^2) (Cuộc sống không phải lúc nào cũng dễ dàng mà 😆) và nó buộc ta phải nâng cấp solution hiện tại lên một phiên bản cao cấp hơn để đạt được độ phức tạp là O(n)

Nếu để ý kỹ hơn một chút thì bản chất của phép nhân loại trừ số ở vị trí i chính là việc ta lấy tích của các số ở trước i nhân với tích của các số ở sau i. Như vậy ta chỉ cần tạo 2 mảng prefix và suffix, mỗi mảng có cùng độ dài với mảng input là n, và nếu xét 1 số ở vị trí i bất kỳ trong mảng input thì mảng prefix tại vị trí i sẽ đại diện cho tích của các số trước i và mảng suffix đại diện cho tích của các số ở sau i. Sau đó tạo mảng output và đi qua từng vị trí tương ứng ở 2 mảng prefix và suffix rồi nhân chúng lại với nhau.

Như vậy ta đã giải quyết được yêu cầu của bài toán đã cho đối với tất cả các phần tử mà chỉ cần sử dụng 3 vòng lặp for riêng biệt. Độ phức tạp về mặt thời gian time-complexity chỉ là O(3n) = O(n) và về không gian space-complexity cũng vậy O(2n) = O(n) khi ta sử dụng thêm 2 mảng phụ là prefix và suffix (Lưu ý trong trường hợp này mảng output không được tính vào space-complexity vì nó nằm trong yêu cầu của bài toán) Và ta cũng không hề sử dụng phép chia nào, như vậy là bài toán đã được giải quyết.

Nhưng khoan 😆 dừng khoảng chừng là 2 giây, đọc kỹ lại đề bài thì ta thấy có 1 phần follow-up (đây là phần nâng cao khi chúng ta đã giải được tối thiểu các yêu cầu của bài toán và không bắt buộc phải làm thực hiện theo) yêu cầu chúng ta giải bài này với space-complexity là O(1) tức là không sử dụng thêm bất kỳ bộ nhớ phụ nào - chính là 2 mảng prefix và suffix. Về mặt logic và idea của giải thuật thì ta vẫn sẽ giữ nguyên, chỉ thay đổi về cách thức lưu trữ mà thôi, vậy làm sao ta có thể bỏ 2 mảng prefix và suffix mà vẫn giữ nguyên được tính toàn vẹn của giải thuật? Hãy cùng theo dõi tiếp ở phần sau nhé!!!

2. Solution & Phân Tích

2.1. Sử dụng kỹ thuật vét cạn - Brute Force

Như đã phân tích ở trên, ta sẽ sử dụng 2 vòng lặp:

• Vòng lặp đầu tiên cố định từng vị trí cần gán kết quả trong mảng ouput gọi là con trỏ i
• Vòng lặp thứ hai đi qua tất cả các phần tử trong mảng input nums và vị trí các phần tử đó phải khác vị trí i mà ta đã cố định ở vòng lặp đầu tiên. Nhân tích luỹ chúng lại với nhau và lưu vào biến tạm nào đó tạm gọi là product
• Sau khi kết thúc vòng lặp thứ hai, ta lưu kết quả của biến product vào mảng output với vị trí i tương ứng.
• Sau khi đi qua hết các vị trí cần tính toán ở mảng ouput, kết thúc chương trình và trả về mảng output.

Time-Complexity: O(n^2)

Space-Complexity: O(1) (Lưu ý mảng output không được tính vào độ phức tạp)

n: số lượng phần tử trong mảng

2.2. Sử dụng 2 mảng Prefix và Suffix

Ta cần tạo 2 mảng prefix và suffix cũng như tính toán các giá trị cho 2 mảng đó, và sau cùng tạo ra mảng output tương ứng. Ta sẽ cần 3 vòng lặp không lồng nhau:

• Vòng lặp đầu tiên sẽ đi qua từng phần tử trong mảng input và tạo giá trị cho mảng prefix tương ứng

• Vòng lặp thứ hai sẽ đi qua từng phần tử trong mảng input và tạo giá trị cho mảng suffix tương ứng

• Vòng lặp thứ ba sẽ đi qua cùng 1 vị trí ở cả 2 mảng prefix và suffix tạm gọi là i, và nhân 2 giá trị đó lại sau đó gán vào mảng output với cùng vị trí i

Time-Complexity: O(3n) = O(n)

Space-Complexity: O(2n) = O(n) (Lưu ý mảng output không được tính vào độ phức tạp)

n: số lượng phần tử trong mảng

2.3. Sử dụng 1 biến thay cho 2 mảng prefix và suffix

Bản chất của việc thay thế này chính là việc ta sẽ tính toán luôn trên mảng output thay vì phải tạo ra 2 mảng prefix và suffix mà vẫn không thay đổi ý nghĩa.

• Ở vòng lặp đầu tiên, thay vì gán kết quả vào mảng prefix, ta sẽ gán thẳng vào mảng output:

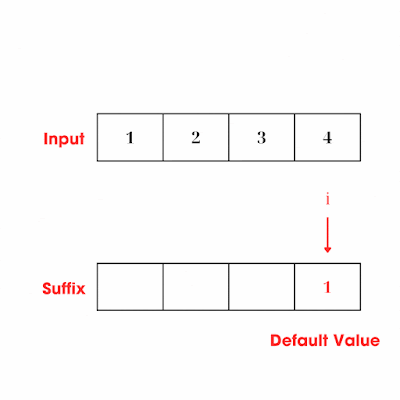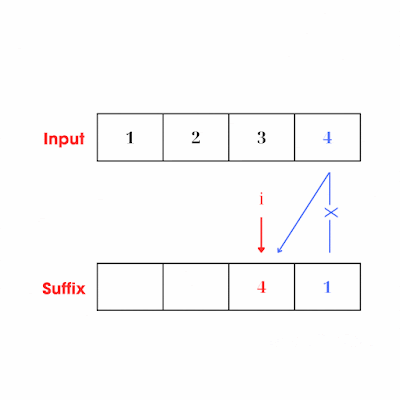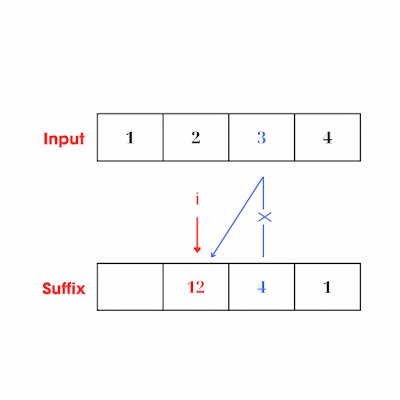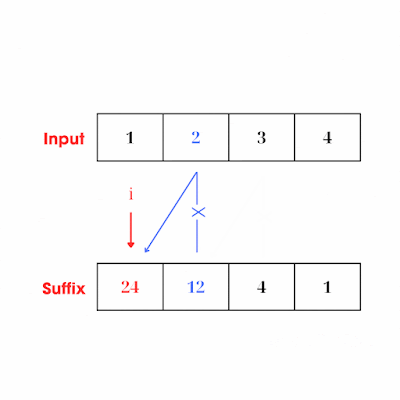
• Như vậy ta đa thay thế được mảng prefix bằng chính mảng output, còn mảng suffix, ta chỉ cần dùng 1 biến tạm currentSuffix, khởi tạo nó bằng giá trị phần tử ở vị trí cuối cùng trong mảng input và tạo 1 vòng lặp duyệt từ vị trí kế cuối về đầu mảng để nhân nó vào các phần tử ở mảng ouput cũng như cập nhật là giá trị cho biến current suffix:
• Tại sao lại bắt đầu từ vị trí kế cuối? Vì vị trí cuối cùng hiện tại của mảng ouput đã thoả điều kiện rồi, nó sẽ không có tích suffix nào đứng sau nó nữa. 
• Tại sao cần khởi tạo currentSuffix = giá trị phần tử cuối cùng của mảng input? Vì lúc này nó đang là suffix của số ở vị trí kế cuối trong mảng ouput.
• Mỗi lần đi qua một phần tử ở vị trí i, ta sẽ nhân currentSuffix cho số tại vị trí i của mảng output, sau đó cập nhật currentSuffix bằng việc nhân nó cho số tại vị trí i của mảng input. Ta cần nhân vào ouptut trước sau đó mới cập nhận biến currentSuffix để đảm bảo điều kiện là tích tại thời điểm đó không bao gồm số ở vị trí đang xét của mảng input. Hay nói cách khác: khi ta xét qua từng vị trí i, thì biến curentSuffix luôn đảm bảo nó chính là tích của các số ở phía sau vị trí i đó. 

Ngoài ra còn có 1 biến thể nữa, là thay vì dùng biến current suffix như trên, ta có thể lưu nó vào chính trong mảng input, và nhược điểm của nó là sẽ làm thay đổi mảng input đã cho, tuy nhiên ở phạm vi của bài toán này thì ta chỉ quan tâm đến mảng output nên solution đó vẫn được chấp nhận.

Time-Complexity: O(2n) = O(n)

Space-Complexity: O(1) (Lưu ý mảng output không được tính vào độ phức tạp)

n: số lượng phần tử trong mảng

3. Code

Mình sẽ dùng java cùng với cách tối ưu nhất để code minh hoạ: